The Illinois Mathematics Lab (previously known as Illinois Geometry Lab) provides a framework for faculty and graduate students to engage local undergraduates in research, administering large-scale research programs each fall and spring semester and smaller programs during the summer months.
Applications for Spring 2024 semester are now closed. The deadline to apply was midnight of Jan. 7, 2024.
Spring 2024 projects are listed below. To receive updates about future projects, join our mailing list here.
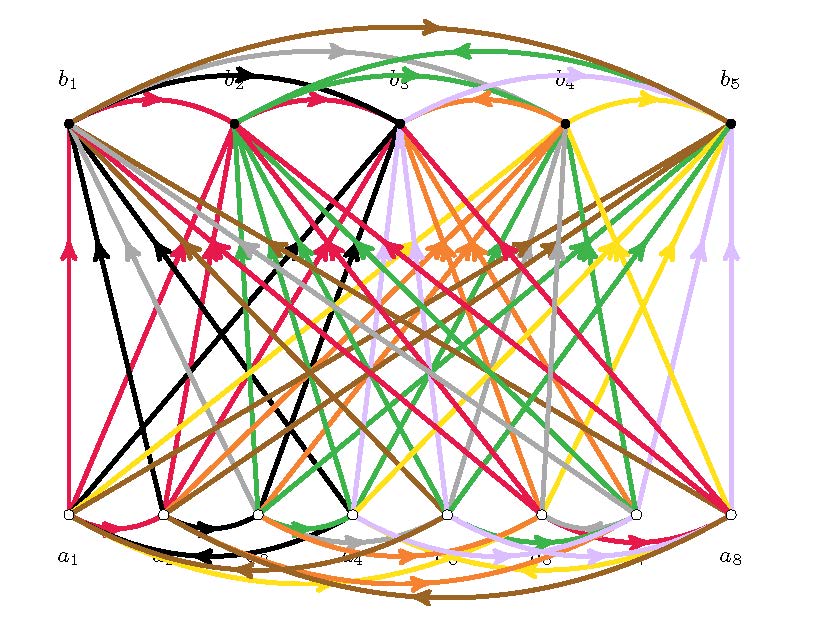
ColorTaiko!
This project originally comes from important open problems in algebra called Kaplansky conjectures, but no knowledge of algebra is needed to participate in the project.
The goal is to popularize these mathematical problems by creating a fun computer game called “ColorTaiko!”, and by distributing it to the general public. In the game, a player will draw edges in a bipartite graph and the program will color those edges in a certain way. The goal of the game is to draw as many edges as possible (ideally all the edges in the complete bi-partite graph) so that the colored configuration (“taiko”) satisfies several specific combinatorial conditions. (If you come all the way to the complete bipartite graph, you solve an important problem in algebra as an additional bonus.)
We are aiming at creating a web-based version of the game first, and hope to write a mobile application as well. Making the game fun and easy to use is an important part of this project. Then we will work on publicizing the game. We also plan to keep improving the game over some time, allowing different sizes for the bipartite graph, creating various new features, multiple levels of difficulty, etc.
- Faculty Member: Igor Mineyev
- Team meetings: twice a week
- Coding prerequisites: To participate in developing the web-based game, it is helpful to have some experience with developing websites and with JavaScript. (We are thinking of using the React framework to write the game, and React uses JavaScript.) To participate in writing the mobile version of the game (preferably both for Android and for iPhone), it is helpful to have some experience with writing and distributing mobile applications.
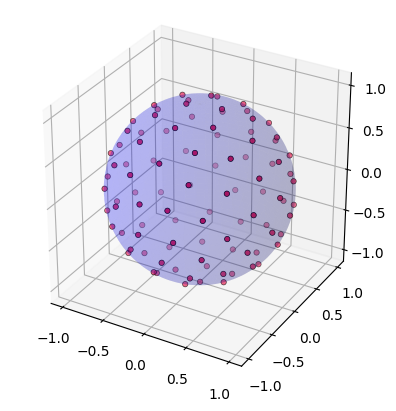
Optimizing capacities: what shape does best when adding a dimension?
Electric charges repel each other by an inverse square force law. What if the force obeys a power law with a different exponent, by embedding the conductor in a higher dimensional space? The project will computationally investigate conjectures for how much the capacity of a conductor can change between two different exponents. In particular, is a disk or ball the optimal shape?
- Faculty members: Carrie Clark and Richard Laugesen
- Difficulty: Intermediate
- Team meetings: weekly
- Course prerequisites: Math 347, comfortable with quantifiers and enjoys thinking about multidimensional space. Background in classical physics is helpful but not essential.
- Coding prerequisites: Basic coding in at least one commonly used language (e.g. Python, Matlab, Mathematica, C, …)
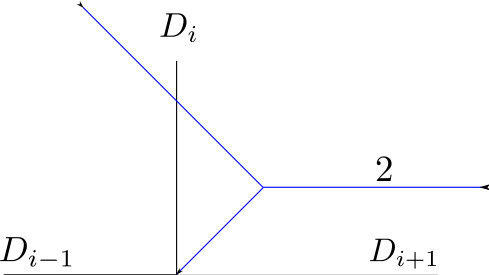
Scattering Diagrams and Broken Lines
What happens if we take Euclidean space, cut it into pieces, and then paste the pieces back together in a new way? Can we get a self-consistent geometry of “straight lines” out of this? In this project we will explore a conceptual framework for such geometries that arise out of the quantum physics of particles and strings. The geometries are described by “scattering diagrams” and our straight lines will be generalized to “broken lines.” Our goal is to develop visualizations for these geometries, and to use computer algebra systems to calculate numerical information about their structure.
- Faculty member: James Pascaleff
- Difficulty: Intermediate
- Team Meetings: weekly
- Course prerequisites: Linear Algebra and Abstract Algebra would be helpful.
- Coding prerequisites: We will be using Mathematica.
Spatial Models of Evolutionary Dynamics
Evolutionary game theory is a mathematical framework for studying how interactions between individuals influences the change in frequency of traits or behaviors in a population. In this project, we will look to use study the evolutionary dynamics of populations with spatial structure, exploring how strategies for social interaction between individuals and the rules for spatial movement of individuals can produce emergent spatial patterns at the population level.
The project will draw upon several different mathematical and computational approaches to study spatial evolutionary dynamics. The group can formulate and simulate discrete stochastic spatial models for describing evolutionary games in a spatial setting, and also derive and analyze ODE and PDE mean-field models for spatial evolutionary games in the limit of infinitely large populations.
- Faculty member: Daniel Cooney
- Difficulty: Intermediate
- Team meetings: weekly
- Course prerequisites: While not required, some material from Math 441, Math 442, or Math 461 may be helpful for certain aspects of this project.
- Coding prerequisites: Some familiarity with Python, Matlab, or another programming language may be helpful, but is not required.
Tennessee Traffic
A standard approach to modelling traffic flow is via various hyperbolic conservation laws. This project will try to match recent data from I-24 in Tennessee to some of these models. Our goal is in part exploration and part pedagogical; traffic problems provide a compelling example for learning partial differential equations.
- Faculty member: Richard Sowers
- Difficulty: Intermediate
- Team meetings: Weekly (perhaps by Zoom)
- Course prerequisite: Math 442 Partial Differential Equations
- Coding prerequisite: Competence in Python
Winter Spaces and the Stabilizer Formalism
Winter spaces are a special class of finite-dimensional ordered vector spaces, and are precisely the objects to consider when determining correctability of a quantum channel. Such spaces are the main ingredients of the famous Knill-Laflamme subspace condition from quantum error correction. One may formulate a stabilizer formalism using classes of Winter spaces. The stabilizer formalism, first introduced by Gottesman, has been generalized to operator quantum error correction, and
more recently, operator algebra quantum error correction. Our goal for term will be to relate special classes of Winter spaces with these more general versions of the stabilizer formalism.
- Faculty Member: Roy Araiza
- Difficulty: Intermediate
- Team Meetings: Weekly
- Prerequisites: Math 416 (Abstract Linear Algebra) required. Background in introductory quantum theory is helpful but not required.
Paintability of Multipartite Graphs
Suppose we play the following game on a graph G. On each turn, an enemy presents us with an induced subgraph H of G, and we must mark an independent set in H. If we know that each vertex of G will be presented to us k times, do we have a strategy to mark all vertices of G? If the presented subgraph H always equals G, then this game is equivalent to the k-coloring problem. However, if our enemy makes our life difficult by presenting subgraphs H that are different from
G, then this game is much harder than the k-coloring problem. In this project, we will consider this problem for multipartite graphs. We will mostly work with complete multipartite graphs, for which this game can be equivalently described in terms of a chip-pushing game.
- Faculty Member: Peter Bradshaw
- Difficulty: Intermediate
- Team Meetings: Weekly
- Prerequisites: Math 412 and 413 are strongly preferred
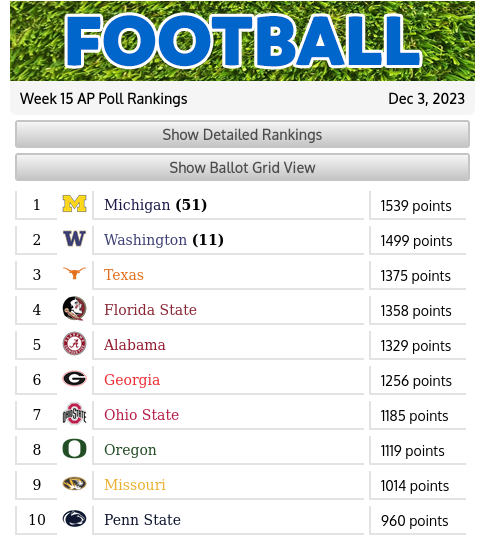
Predictability and Competitiveness in Sports Leagues
Sequences of wins and losses of sports teams over the course of a season provide a rich source of real-world pseudo-random sequences to explore from a variety of angles. In this project we will focus on issues such as the predictability of games, the effect of home advantage on game outcomes, and the parity and competitive balance among teams in a given sports league. We will develop mathematical tools to quantify phenomena of this type and then apply these tools to real world data from a variety of teams sports, focusing primarily on collegiate sports such as NCAA Division 1 College Football and College Basketball. This project continues and expands on the themes of the Spring 2023 and Fall 2023 IGL projects titled “Win/loss sequences in sports leagues”, which were focused on professional sports leagues. However, familiarity with these earlier projects is not expected. The project has a theoretical component involving reading background literature,
but the bulk of the work will be on the coding side. All participants should be proficient with Python and ideally should have some experience with large scale coding projects. Knowledge of the sports mentioned is not required. However, if you are very knowledgeable in one of the mentioned sports, please mention this in your application.
- Faculty Member: AJ Hildebrand
- Difficulty: Intermediate
- Team Meetings: Weekly
- Prerequisites: A high level of proficiency with Python is essential. There are no hard course prerequisites; any needed background in probability and statistics can be acquired during the course of the project.
- If you have a Github site, please mention it in your application. Experience with webscraping tools may be helpful for certain aspects of the project, but is not required.
Developing Inclusive Outreach Materials in Mathematics
An important part of IGL’s mission is to support departmental efforts to engage local communities through outreach and to share our passion for mathematics beyond our campus. In recent years we have organized visits at local schools and participated in public forums, such as a math outreach table at the Urbana Farmers Market. In this project, we’ll continue to develop mathematics outreach materials with an emphasis on inclusion. Champaign-Urbana schools have a significant number of English language learners who speak Spanish or French, so we hope to make materials accessible in those languages, and also to think more broadly about how outreach efforts can be as inclusive as possible. Group members will decide what areas of mathematics the group will focus on, and will learn some new mathematics themselves in the process! Ideally, we’ll also generate ideas and contacts for future expanded outreach events.
- Faculty Member: Karen Mortensen
- Difficulty: Basic
- Team Meetings: Twice per Week
- Prerequisites: Interest in mathematics outreach and/or education is required. Knowledge of Spanish or French is desirable, but not required.
Quantum Gates for Quantum Noise
We will learn about two type of noise for quantum devices: individual qubit errors, and so called collective error which appears naturally in quantum devices. After revealing some of the basic theory, we start with a given resource set and find a concrete family of quantum circuits simulating the above noise model. The aim of the research is to write a quantum program and try to let it run on either the IBM quantum computer or another online simulator. We will effectively do one example of quantum compilation-and learn a lot of math on the way.
Faculty Member: Marius Junge
Difficulty: Intermediate
Team Meetings: to be determined
Prerequisites: Linear algebra and the willingness to apply it. It would be helpful to have some familiarity with quantum mechanics either through coursework or individual study.
(Linear) Poisson structures and their cohomology
Poisson brackets naturally arises in the context of Hamiltonian mechanics to describe the Hamiltonian equations of motions. This project focuses on linear Poisson brackets in dimension 4. The goal of this project is to understand the underlying foliation, infinitesimal automorphisms and deformations by means of the associated cohomology groups, i.e. Poisson cohomology, for some of the linear Poisson brackets. The objective of the project is to compute some of these groups and write a program which does some of the computations for us.
Faculty member: Florian Zieser
Difficulty: Advanced
Team meetings: Biweekly
Prerequisites: Math 416 and Calculus 1-3 or equivalent. Additionally, any courses in differential geometry, tensor calculus and algebra would be very helpful. Also some knowledge of python or similar programming languages would be good.