The Mrs. E. J. Hoover Program for Advanced Students in Mathematics consists of summer research projects for advanced undergraduates. These research projects are designed to bridge the gap between advanced undergraduate courses in mathematics and graduate-level research in mathematics. The goal is to provide challenging research opportunities for future graduate students in mathematics. The project runs for six weeks in the summer, and the research team consists of one faculty mentor, one graduate student (the team leader) and several undergraduate students. Hoover projects are at a high level of mathematical sophistication, while still being approachable enough such that undergraduate students can produce real results within the given time frame.
The dates of the project are May 28-July 5, 2024. Participating undergraduate will receive a stipend of $1500 deposited to their student account.
Requirements
- Participating students are required to be on campus during the project (May 28-July 5, 2024) and are expected to devote 20 hours/per week to the project.
- Participants must be undergraduate students at the University of Illinois. Preference is given to Math majors and Math&CS majors.
- See below for mathematical prerequisites.
To receive updates about future projects, join our mailing list here.
Summer 2024 project
Geodesics on integral affine manifolds
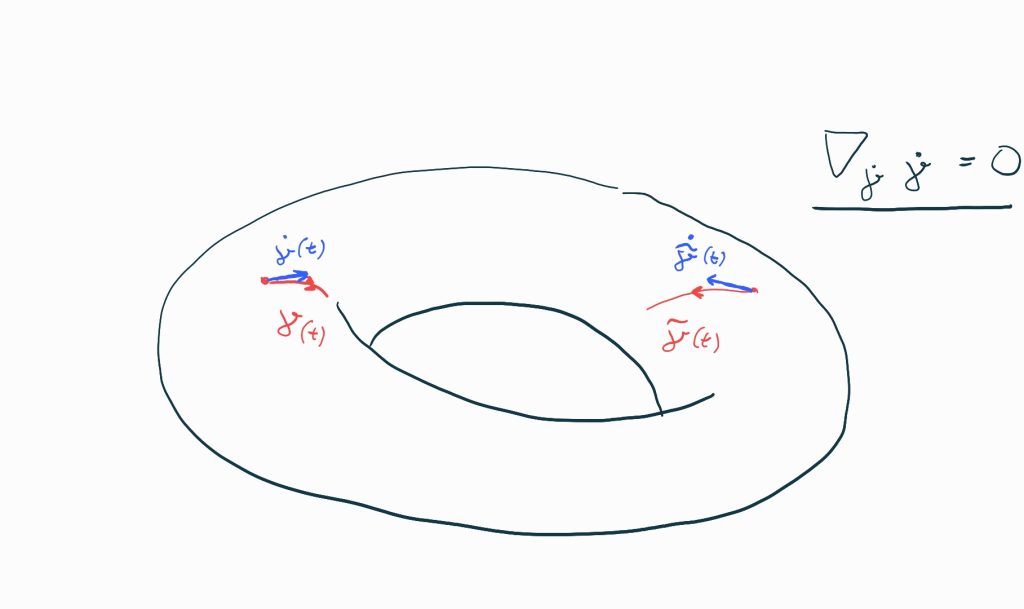
Integral affine manifolds naturally arise in symplectic geometry and for integrable Hamiltonian systems. These manifolds come naturally equipped with a flat connection induced by the integral affine structure. In this project we want to study the geodesics associated to the connections on integral affine manifolds in dimension 2. We first recall the necessary theory for manifolds, before focusing on integral affine manifolds and their special properties. If time permits we can also investigate such manifolds in dimension 3.
- Faculty Member: Florian Zeiser
- Mathematical prerequisites: A proof based course (Math 347) as well as linear algebra (Math 416) and Calculus 1,2,3. Some knowledge of surfaces (Math 423) and tensor calculus (Math 481) is beneficial but not strictly necessary.
- Coding prerequisites: None